Writing a Sudoku Solver using Backtracking.

Today, we are gonna talk about programming a Sudoku Solver. I am one of those people who really enjoys solving Sudoku puzzles so writing a program that can do it for me had always been on my “projects-I-would-someday-like-to-do” list. The day finally arrived and I successfully got around to coding up my own Sudoku solver.

What am I trying to solve?

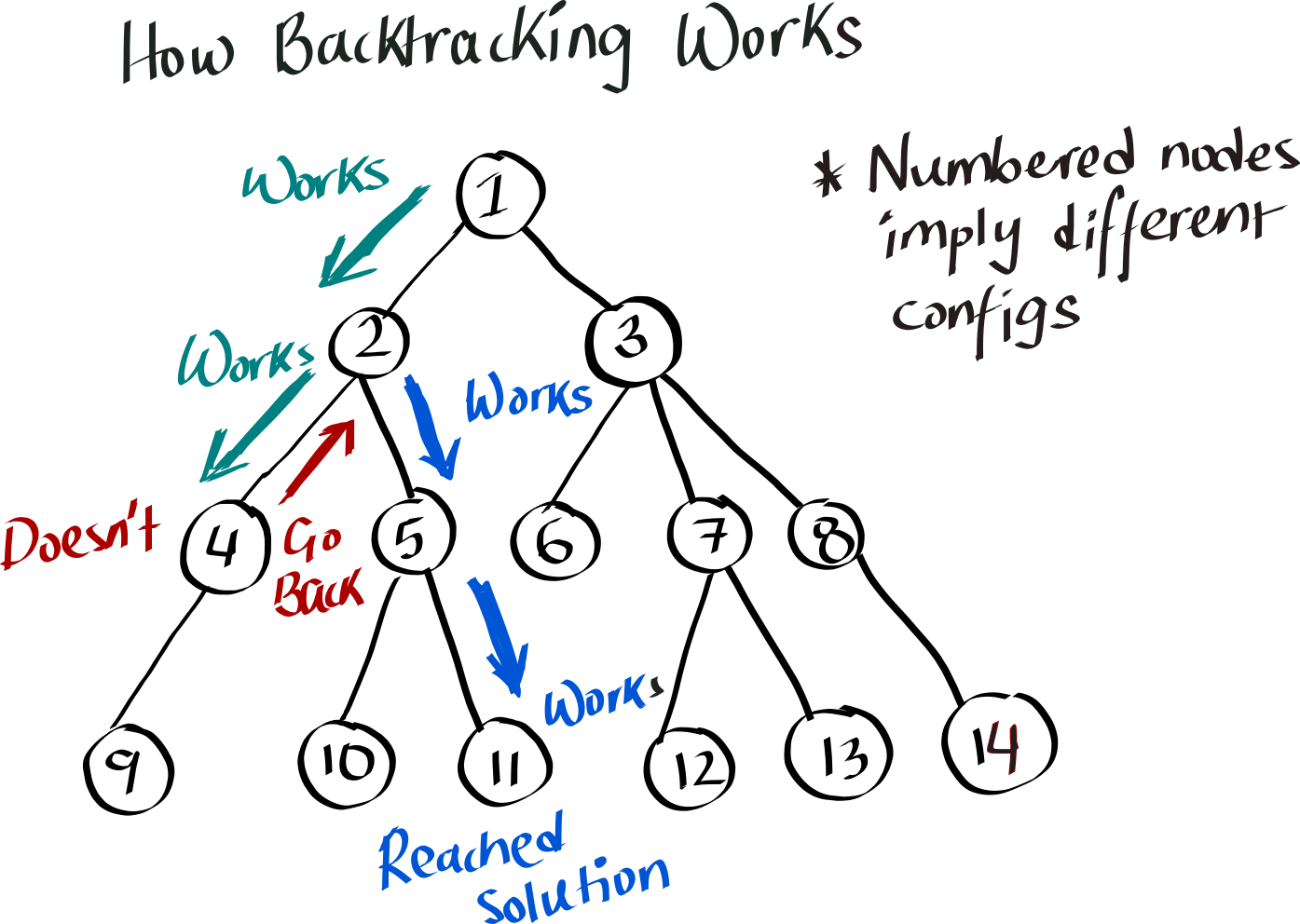
So let’s think about this problem a little bit. To start off with, each empty square on the board can have any number between 1-9. And we cannot have repeating numbers in the same row, column or sub-grid. So if we start laying down numbers -starting from 1 through 9- on the board while obeying these rules, we’ll have a bunch of different intermediate configurations of the board that may or may not reach the solution. If you work out all these possible configurations, one number at a time, things will start looking like a tree or graph with multiple branches, where only one path will lead to the correct solution.

Example graph of how all possible configurations will map out.

What algorithm to use?

So, Sudoku can be classified as a classic search problem where you go through all the possible states in a graph to find the optimal solution. There are tons of ways to search through a graph, but backtracking search is the most efficient way to solve a Sudoku. Instead of working out all the possible states - whether it leads to solution or not - backtracking builds the solution by taking step, see if it could lead to a solution, if not step backwards (backtrack) and try something else.

How to code this?

Now let’s dive into the implementation. My Python code can be found here on GitHub. I’ll be using Python looking pseudo code here so that it is easier to follow along.

Let’s start with setting the scene first. I am going to create some variables and lists contained in a class.

class Sudoku():
# Initialize vars and lists
    def __init__(board): 
        Board is an input
        rows,columns,boxes = a list of range 1-9
        values = a list of range 1-9
        backtracked = 0

I created lists to enumerate each row, column and sub-grid (box). The board or puzzle to be solved is fed into the class. I also created a list of all possible values 1-9. Let’s also create a variable to keep count of how many times we have backtracked so that we can run some tests later.

Now let’s create some functions to detect empty squares and check if a value satisfies the rules/constraints.

• Create a function to detect if a cell is empty. It should return True if empty and False if full. An empty cell has a value of 0 in the input puzzle board. Starting from the top left corner of the board - cell [0, 0] - it will check each cell until it finds an empty cell. A variable (technically a list) is passed into the function that will store this empty cell location for later use.

    def find_blanks(count):
        # Input: count is a list passed into the function to save current empty cell location
        for each cell on the board:
            if board[cell] = 0
                count = cell #Save cell as count
                return True
        return False

• Create functions that returns “legal” values given the already existing numbers in a row, column and sub-grid/box. This narrows down the domain of possible values. We’ll write three functions that works out the domain based on the row, column and box individually first. And then we will have a fourth function that gets rid of any repeating numbers from all three domains combined to trim down the list of possible candidates even further.

    # Returns domain after checking row constraints
    # Input: Current row
    def check_rows_dom(row):
        domain = values # Values created earlier
        for each cell in row:
        # Get rid of any number already in this row
            if board[cell] in domain:
                domain.remove(board[cell]) 
        return domain

    # Returns domain after checking column constraints
    # Input: Current column
    def check_columns_dom(column):
        domain = values
        for each cell in column:
            if board[cell] in domain:
                values.remove(board[cell])
        return domain

    # Returns domain after checking box constraints
    # Input: Current row and column 
    def check_boxes_dom(row, column):
       domain = values
       for each cell in a box:
                if board[cell] in values:
                    values.remove(board[cell])
        return domain

It can be a little tricky to figure out how to define and check within each sub-grid or box given the cell location if you are a naive programmer like myself. I encourage you to look at my code if you need ideas on how to do this.

  # Find domain of values that meet all constraints
  def find_constrained_dom(cell): # cell = [row, column]
      # Call the previous functions 
      row_dom = check_rows_dom(row)
      column_dom = check_columns_dom(column)
      box_dom = check_boxes_dom(rows in box, columns in box)
      domain = intersection of row_dom,column_dom,box_dom
      return domain

The final domain contains the intersection - or common- elements from each of the individual domains found from checking each constraint. These values satisfy all the constraints - these numbers are non-repeating in the corresponding row, column and box of each empty cell.

We are now ready for some backtracking. Let’s create a function for this. This will be a recursive function. Recursion is when you call the function within itself, so it is called again and again until a certain condition is met.

• It starts with looking for an empty cell. It quits when no empty cells are left.

• It finds the domain for the cell, given the current board configuration.

• It then checks each value in the domain.

• Recursion is used to call the function again when a value is picked to move on to the next step.

• If a value happens to not work (meet constraints), it backtracks, sets the cell back to “empty” and tries the next value in the domain.

# The backtracking function
def backtracking(count):
    Input: Pass a list to the find_blanks() to save the location of current empty cell 
    # Start searching for blank cells
    if not find_blanks(count):
        return True # If no blanks found, stop else continue
    
    # Set current cell to the first empty cell found
    cell = count 
    
    # Get domain for empty cell
    cell_domain = find_constrained_dom(cell)
    
    # Start the search
    for each number in cell_domain:
        board[cell] = number
        
        # Recursion
        if backtracking(count):
            return True
        
        board[cell] = 0 # Reassign empty
        
        # if backtracked increment variable: backtracked
        if board[cell] = empty:
            backtracked =+ 1 
        
    return False # Necessary to trigger recursion

Let’s run some tests

I went over to websudoku.com to look up some Sudoku puzzles of varying difficulty to test my solver. They have puzzles rated in four levels of difficulties: Easy, Medium, Hard and Evil. I picked one from each category. I used the number of times the algorithm backtracked to see if my program feels the same way about how hard each puzzle is to solve. The higher the number of times it backtracked, the more difficult the puzzle should be since it would take much longer to reach a solution.

Here are the results.

It’s interesting to see that how the algorithm’s “perception” of difficulty is different from humans. Both are measured by the amount of time taken to find the solution. The Evil puzzle turns out to be the second most easiest puzzle, where as the Medium puzzle turned out to be most difficult to solve. For my next blog post, I intend to tweak this algorithm to make it more efficient. We’ll see if those changes have any effect on these results.

Hope you enjoyed this post. Stay tuned for the next one!